Thermoelectric Semiconductor

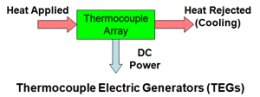
Direct Conversion of Heat Energy to Electrical Energy (1)

Thermocouple Electric Generators

When any electrical conductor is subjected to a thermal gradient, by heating one end while maintaining the other end at a low temperature, it will generate a voltage between the hot and cold ends. This is known as the Thomson effect and is principle used for the direct conversion of heat energy into electrical energy.

Thermocouples

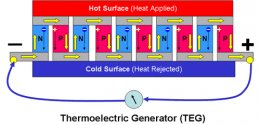
The phenomenon of thermoelectricity was first observed in 1821 by by the German physicist Thomas Johann Seebeck who noticed that when a loop was made from wires using two dissimilar metals, a voltage appeared between the junctions of the wires if one junction was hotter than the other. Such a loop made with dissimilar metals became known as a thermocouple and the phenomenon was named the Seebeck effect in his honour. The voltage generated by the thermocouple is very small and many thermocouples are required to make a practical thermoelectric generator.

Semiconductor Thermocouples

For over a century thermocouples were made from metallic conductors and though many different metals were investigated, efficiencies rarely exceeded 3%. With the advent of semiconductors the efficiency of thermoelectric generators was greatly increased and by the 1950's, generator efficiencies had reached 5% and Peltier cooling from ambient to below 0°C was achieved.

Thermocouple Performance

The Seebeck Coefficient

Kelvin showed that for small temperature differences the voltage produced between the hot and cold ends of a single conducting rod is proportional to the temperature difference between the two ends. The proportionality constant S is now known as the Seebeck coefficient and is defined as:

S = Δ V / Δ T

where Δ T is the temperature difference between the two ends of a material and Δ V is the thermoelectric voltage generated. It is thus a measure of the magnitude of an induced thermoelectric voltage in response to a temperature difference across the material.

For most conductors the voltage created is tiny, just a few microvolts per degree difference in temperature. For semiconductor materials the coefficient may be between 100μV/°K and 300μV/°K, in any case still very small. This is mainly because the kinetic energy of the charge carriers in semiconductors is strongly temperature-dependent, whereas in metals it is not so strongly temperature-dependent.

More generally the Seebeck coefficient is non-linear, and depends on the material of the conductor, its molecular structure and the absolute temperature. The Seebeck voltage does not depend on the temperature distribution along the conductor but only on the temperature difference between the ends. The Seebeck coefficient is often incorrectly referred to as the thermoelectric power or thermopower (it is a voltage not a power).

Thermoelectric Materials

Ideal thermoelectric materials should have the following properties:

• High Seebeck coefficient S - to get the maximum output voltage per degree of temperature difference.
• High electrical conductivity σ - to minimise Joule heating
• Low thermal conductivity λ - to restrict the diffusion of the heat across the device in order to maintain a large temperature gradient.

For comparison purposes the usefulness of thermoelectric materials for electricity generation as well as for heating and cooling can be characterised using a figure of merit incorporating these properties.

The figure of merit Z of a thermoelectric material is a measure of its efficiency as an energy conversion component and is defined as :

Z = σS2

Materials with high thermoelectric figures of merit are typically heavily doped semiconductors and for many years the best materials had a figure of merit of around 1. Recent advances in materials science have increased this number to around 4.

Thermocouple Output Voltage

In practice, to extract useful current from the ends of a conducting rod requires the connection of wires to the end points, essentially forming a second conductor in parallel between the heat source and the heat sink. The voltage generated in the wires will thus oppose the voltage generated across the rod and the net voltage generated will be the difference between the voltages generated across the rod and across the wires. The circuit arrangement containing two dissimilar metals forms a thermocouple.

The thermoelectric voltage generated in a single conductor is already very small. The connection of wires across the conductor to extract the electrical energy introduces an opposing voltage in the circuit so that the net useful voltage available is even smaller.

The diagram below illustrates the voltage developed by the thermocouple.

The voltage difference, V, produced across the terminals of an open circuit made from a pair of dissimilar metals, A and B, whose two junctions are held at different temperatures, depends on the temperature difference between the hot and cold junctions, (Th - Tc).

Because both conductors are subject to the same temperature difference the net voltage generated will be the difference between the voltage generated across each conductor.

Thus the net voltage developed is given by:

V = ∫TcTh (Sb(T) - Sa(T)) dT

where Sa and Sb are the Seebeck coefficients of the metals A and B, and Th and Tc are the temperatures of the hot and cold junctions.

For small temperature differences the Seebeck coefficients are effectively constant over the temperature range and the above formula can be approximated as:

V = (Sb - Sa) x (Th - Tc)

This is the physical basis for a thermocouple, which is used often for temperature measurement and in special circumstances for power generation. See Practical Devices below