Resistivity Semiconductor

The fundamental relationship that explores a materials opposition to electron flow was first derived in 1826 by Georg Ohm, a German physicist and mathematician. Ohm's Law is represented by the following equation:

It is important to note that resistance is dependent on the specific geometry of a material specimen as seen in Figure 2.

Residual Resistivity and Matthiessen's Rule

At low enough temperatures, the degrees of thermal vibration are not yet activated meaning the residual resistivity of a metal is a collection of all other scattering sites present in the material specifically defects and impurities. With polycrystalline metals, there will be a number of sources of defects in the microstructure including Grain boundaries, dislocations, and vacancies. Along with defects, impurities in a metal can host a scattering site. In 1864 Augustus Matthiessen, a British chemist and physicist, was the first to incorporate all of these aspects into the resistivity of a metal. Matthiessen's Rule is as follows:

[rho=rho_{th}+rho_{imp}+rho_{def}]

where ρth is the resistivity due to temperature, ρimp is the resistivity due to impurities and ρdef is the the resistivity due to defects. While temperature, defects, and impurities do in fact contribute to resistivity, some deviation from the simple summation postulated by Matthiessen has been reported for specific metals.

Resistivity of Alloys

From Matthiessen's Rule it was seen that the resistivity of a metal was influenced by the impurities present. This portion of the resistivity begins to have a significant contribution when metals are alloyed together. An alloy can be viewed as a metal with a large number of impurities, meaning there is a great deal more scattering sites to increase the residual resistivity of the metal. The result of this increase is a translation of the plot in figure 3 upward. At varying compositions of a simple binary alloy, the resistivity of the system is a linear interpolation of the resistivity of each pure metal. If the system exhibits an energetically favorable phase transition that results in a more ordered structure than that of the solute atoms in solution, a drop in resistivity at that composition will be observed. An example of a binary system that has ordered phases that affect resistivity is copper and platinum.

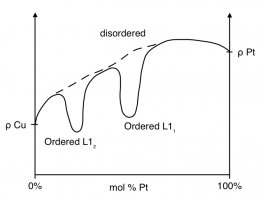
Figure 4. Resistivity of the binary system of copper and platinum at 500 K as a function of composition. The dashed line models standard linear interpolation of the two pure metals while the solid line represents the actual resistivity due to the formation of ordered phases.